golang笔记

分析 Go 标准库中的 WaitGroup 实现

　　在 Go 语言中，goroutine 的重要性不言而喻，为了更好的控制 goroutine 的运行，在 Go 语言的标准库中提供了一系列的控制手段，WaitGroup 就是其中很常用的一个。本篇来分析一下 WaitGroup 的具体实现。

用法

　　在分析 WaitGroup 的实现之前，先简单看一下它的用法。它的用法非常简单，因为它只有 Add/Done/Wait 这三个对外的方法可供调用。

1
2
3

func (wg *WaitGroup) Add(delta int)
func (wg *WaitGroup) Done()
func (wg *WaitGroup) Wait()

　　来看一个使用 WaitGroup 等待子 goroutine 运行结束的简单示例。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

func main() {
    wg := sync.WaitGroup{}
    wg.Add(1)
    go func() {
        defer wg.Done()
        for i := 0; i < 5; i++ {
            println(i)
        }
    }()
    wg.Wait()
}

　　本例子中，首先创建了一个 WaitGroup 变量，然后通过其 Add 方法指明了它需要等待结束的 goroutine 数量。在启动的 goroutine 里面调用了 WaitGroup 的 Done 方法来表示一个 goroutine 执行完成了。主 goroutine 里面使用了 Wait 方法进行等待，当所有要等待的 goroutine 都结束以后，Wait 方法返回，整个函数执行完毕。

结构

　　WaitGroup 的结构很简单，维护了三个不同的计数，分别是 counter、waiter 和 semaphore，counter 记录了要等待结束的 goroutine 个数，waiter 记录了等待在该 WaitGroup 上的 goroutine 的个数，semaphore 被用作信号量。

1
2
3
4
5

type WaitGroup struct {
    noCopy noCopy
    state1 uint64
    state2 uint32
}

　　但是在 WaitGroup 的结构里并没有直接以这三种变量命名的成员，noCopy 用来告诉代码提示器本结构体变量不能进行值复制，这个暂且略过。在结构体内使用了一个 uint64 和一个 uint32 两个数字来表示了这三个变量。
　　之所以这样设计，是为了同时兼容 32bit 和 64bit 环境下的原子操作。在 WaitGroup 的实现中将 counter 和 waiter 两个部分当作了一个 uint64 变量进行操作，semaphore 当作一个 uint32 变量进行操作。
　　在使用 64bit 的原子操作方法进行操作时，需要被操作的变量是对 64bit 对齐的，在 64bit 环境下这个是没有问题的，但是在 32bit 环境下 uint64 也是对 32bit 进行对齐的，这就导致实现在 32bit 下变得不再可靠。
　　WaitGroup 通过一个巧妙的设计处理了这个问题，在 32bit 环境下，state1 向 32bit 对齐，但是从 state1 的后 4 个字节开始，到 state2 结束，这 8 个字节是向 64bit 对齐的，是可以使用 64bit 的原子操作进行操作的。
　　正是依赖于这个情况，WaitGroup 在 32bit 时，使用 state1 的前 4 个字节来表示 semaphore，使用 state1 的后 4 个字节和整个 state2 来表示 counter 和 waiter 的集合体。当在 64bit 时，使用整个 state1 表示 counter 和 waiter 的集合体，使用整个 state2 来表示 semaphore。

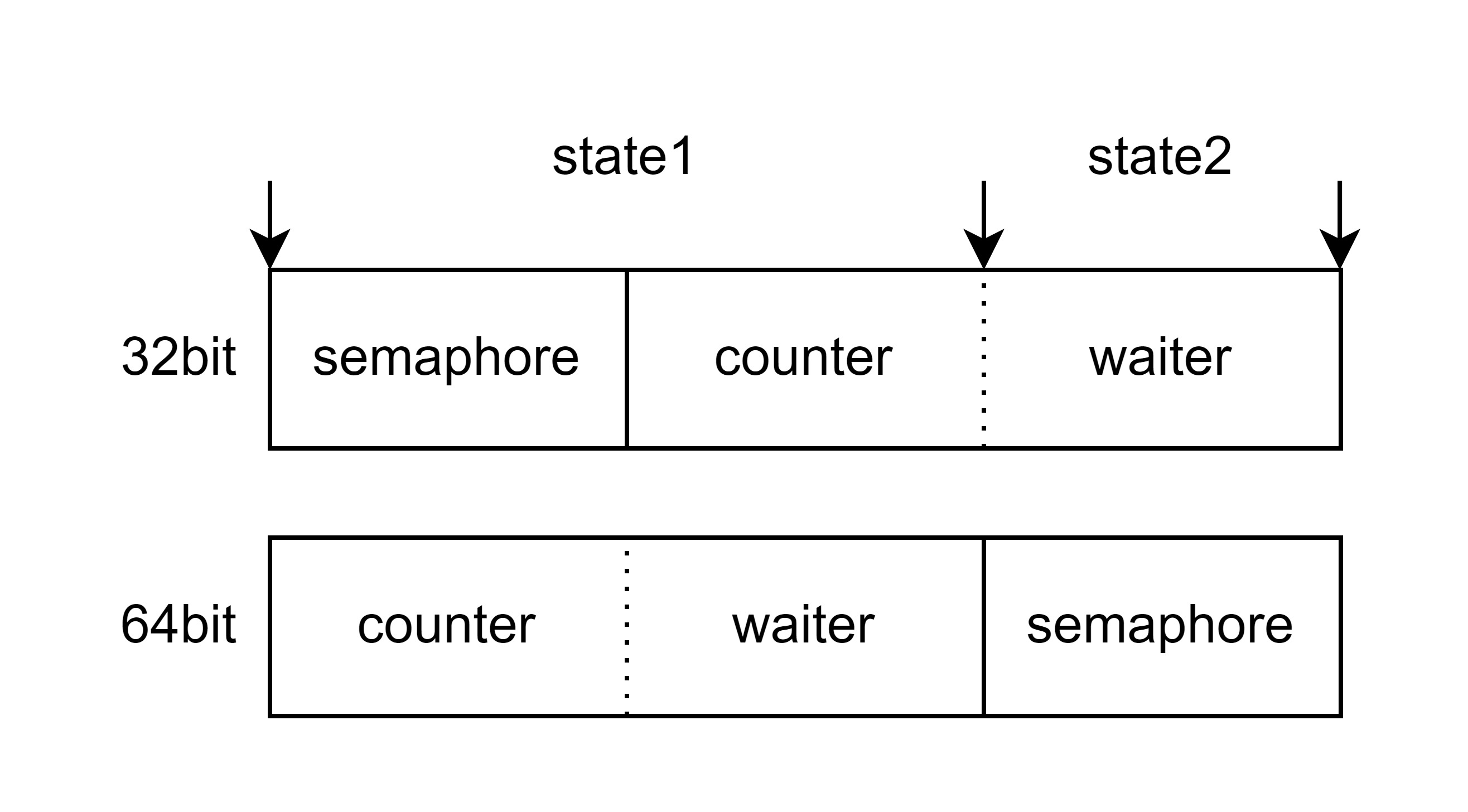
waitgroup_struct

　　在需要获取这两部分的地址的时候，WaitGroup 有一个 state 方法做了这件事情。

1
2
3
4
5
6
7
8

func (wg *WaitGroup) state() (statep *uint64, semap *uint32) {
    if unsafe.Alignof(wg.state1) == 8 || uintptr(unsafe.Pointer(&wg.state1))%8 == 0 {
        return &wg.state1, &wg.state2
    } else {
        state := (*[3]uint32)(unsafe.Pointer(&wg.state1))
        return (*uint64)(unsafe.Pointer(&state[1])), &state[0]
    }
}

　　state 方法会判断当前环境下内存对齐的状态，然后按情况分开返回两部分的指针。第一个返回值是 counter 和 waiter 的集合体的指针，第二个返回值是 semaphore 的指针。

Add && Done

　　之所以将 Add 方法和 Done 方法合在一个分节里，是因为 Done 只是对 Add 的简单调用而已。本节主要来分析一下 Add 方法即可。
　　从一开始的例子中可以看出，Add 方法的作用是修改当前等待结束的 goroutine 的数量，它接受一个参数 delta，这个参数可正可负，也就是说 Add 其实不仅可以增加也可以减少计数，只是一般不会直接使用 Add 来减少计数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

func (wg *WaitGroup) Add(delta int) {
    statep, semap := wg.state()
    state := atomic.AddUint64(statep, uint64(delta)<<32) // 使用原子方法修改
    v := int32(state >> 32) // 通过移位得到 counter
    w := uint32(state) // 通过类型转换得到 waiter
    if v < 0 {
        panic("sync: negative WaitGroup counter")
    }
    if w != 0 && delta > 0 && v == int32(delta) {
        panic("sync: WaitGroup misuse: Add called concurrently with Wait")
    }
    if v > 0 || w == 0 {
        return
    }
    if *statep != state {
        panic("sync: WaitGroup misuse: Add called concurrently with Wait")
    }
    *statep = 0
    for ; w != 0; w-- {
        runtime_Semrelease(semap, false, 0)
    }
}

　　以上的源码中删掉了 race 检查相关的代码。从上面的源码中可知 Add 不仅修改了计数器 counter，同时也做了计数检查。
　　如果上面的 if 分支都没有匹配的话，说明 counter 已经等于 0 且 waiter 不等于 0，此时会将 counter 与 waiter 的集合体 statep 重置为 0 方便后续复用该 WaitGroup，然后根据 waiter 保存的计数，依次调用 runtime_Semrelease 触发信号 semap，唤醒所有等待中的 goroutine。

1
2
3

func (wg *WaitGroup) Done() {
    wg.Add(-1)
}

　　因为 Add 的处理已经很完善了，所以 Done 方法的实现只是用 -1 作为参数调用 Add 使 counter 计数减一，如果计数归零，Add 也可以正确处理。

Wait

　　Wait 的作用是将调用该方法的 goroutine 阻塞，等 WaitGroup 中的 counter 计数归零后，会将其唤醒继续执行 Wait 之后的代码。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

func (wg *WaitGroup) Wait() {
    statep, semap := wg.state()
    for {
        state := atomic.LoadUint64(statep)
        v := int32(state >> 32)
        w := uint32(state)
        if v == 0 {
            // Counter is 0, no need to wait.
            return
        }
        // Increment waiters count.
        if atomic.CompareAndSwapUint64(statep, state, state+1) {
            runtime_Semacquire(semap)
            if *statep != 0 {
                panic("sync: WaitGroup is reused before previous Wait has returned")
            }
            return
        }
    }
}

　　以上是去掉 race 检查以后的 Wait 源码。在 for 循环中使用 CAS 原子操作，比较并修改 statep 的值，将 waiter 的计数进行累加。然后执行 runtime_Semacquire 将自己阻塞在信号 semap 上，等待唤醒。

小疑问

为什么要将两个计数合并

　　考虑一下为什么要煞费苦心将 counter 和 waiter 这两个计数合并成一个 uint64 类型的值？似乎可以用两个 uint32 的值来分开表示，然后在操作各自的时候都使用 uint32 的原子操作即可，这样也不用考虑内存对齐的问题。
　　这样做是因为 counter 和 waiter 这两个计数在使用时需要匹配才行，如果将这两个计数分开表示，那么就要用两次原子操作读取，在这两次原子操作之间就可能产生一些变化使 counter 和 waiter 不再匹配，从而导致一些难以预料的问题。

1
2
3
4
5
6
7
8

func main() {
    wg := sync.WaitGroup{}
    wg.Add(1)
    go func() {
        wg.Done()
    }()
    wg.Wait()
}

　　比如上面这个简单的例子，在 counter 和 waiter 使用原子操作一次读出的情况下，不管 Done 和 Wait 谁先谁后执行，都不会有什么问题。但是如果分开读取的话，整个过程就会分为四步：

  1. Wait 读取 counter，判断 counter 是否等于 0，如果为 0 则直接返回
  2. Wait 修改 waiter，将 waiter 加一，并且阻塞自己
  3. Done 修改 counter，将 counter 减一
  4. Done 读取 waiter，判断 waiter 是否等于 0，如果为 0 则直接返回

　　如果按照 1->3->4->2 的顺序执行的话，则此时会发生死锁，第 4 步判断 waiter == 0 直接返回了，后面执行的第 2 步中 Wait 等待的唤醒信号将永远也不会到来。

为什么 Wait 需要无限循环

　　考虑一下为什么在 Wait 中要用一个无限的 for 循环来包裹住整个处理呢？按常理来看似乎完全不需要 for 循环的包裹也可以正常执行。
　　原因是 CAS 操作是有可能不成功的，因为 Wait 并不一定只有一处调用，如果在 LoadUint64 之后，CAS 之前，有其它地方也执行了 Wait 操作，那么 statep 指向的值就被改变了，但是 state 还是旧值，所以 CAS 就无法成功执行了。用一个无限的 for 循环包裹住这一部分操作，可以保证 CAS 操作最终一定会成功。

golang
Licensed under CC BY-NC-SA 4.0
© 2022 - 2024 放学后茶会
Built with Hugo
主题 Stack 由 Jimmy 设计